回転慣性(rotation inertia)の計算
一般に回転慣性(以下,単にIと記す)が必要になるのは,特に床のIに限定すれば,捩れの自由度を考慮した振動解析をするときだと思います。
私も過去に数え切れないほど計算してきました。
しかし,今頃になって「大昔に行った計算はあれでよかったのか?」と疑問を抱くようになり,近日中に久しぶりの捩れ振動解析を行うこともあって,今更ながら検証を行いました。
私も過去に数え切れないほど計算してきました。
しかし,今頃になって「大昔に行った計算はあれでよかったのか?」と疑問を抱くようになり,近日中に久しぶりの捩れ振動解析を行うこともあって,今更ながら検証を行いました。
回転慣性Iは,床面形状が矩形で質量分布が均質であれば,下式のように,短辺長さと長辺長さをそれぞれ自乗して足し合わせ,それに質量を乗じて12で割れば,Iは簡単に求められます。
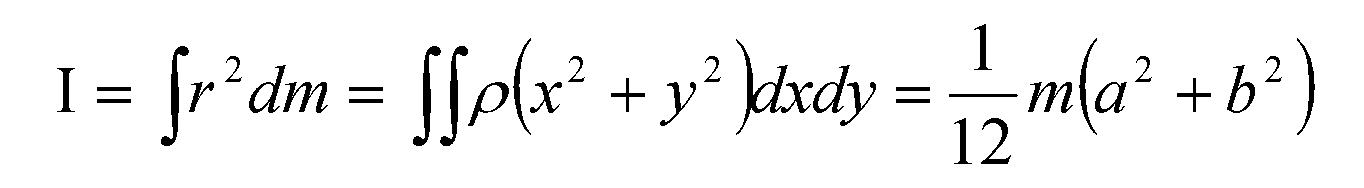
ただし,矩形以外の形状では数値積分する必要があり,十分な精度を確保しようとすると,「細かく床を分割して,かけて,足す」という作業を何百回も繰り返すことになります。プログラム化したくなる計算の代表例ですね。
というのも,約10年前に一貫構造計算結果を元に回転慣性を計算するツールを作りましたが,当時の私は安直に,節点〜重心間距離の自乗に地震用節点重量を乗じて足し合わせました。
これが一貫構造計算結果を用いる上で最も簡便で,質量分布の偏りも表現できる方法だったからです。当時は特に違和感も感じませんでした。
しかし,比較的最近になって・・・
「重心とは対象物の重量中心なんだから,積分する際のrは細かく分けた床の重量中心と床全体の重心との距離でなければおかしい」
「節点重量と節点座標を用いた計算では,rが長くなってしまう」
「柱割りの少ない建物で誤差が大きいんじゃないか」
と思い始めたんです。
そこで,10m角の正方形で4本柱(=4節点),重量は1000kNという簡単なモデルで検証してみます。
質量分布は均質で,重心と図心が一致する(Gx=5m,Gy=5m)とします。
I=1/12×1000kN×(10^2+10^2)=16667kN・m^2(これを精算値とします)
矩形の計算式では簡単にIが求まります。
このモデルで,rを節点位置〜重心間距離として求めると,各節点重量は250kN,距離はXYともに5m(r=7.07m)となり,I=50000kN・m^2になります。精算値の実に3倍です。
こんな極端なモデルは現実には極めて稀でしょうが,やはり柱割りの少ない建物では注意が必要であることがわかります(精算値を超えること事態が明らかに間違いです)。
今度は,積分する際の短冊幅を5m(4分割)とし,分割した各床の重量中心と全体の重心間距離をrとすると,距離はXYともに2.5m(r=3.54m)となり,I=12500kN・m^2(75%)となります。精算値を超えはしませんが,25%減では精度が低すぎます。
短冊幅1m(100分割)ではI=16500kN・m^2(99.00%),0.5m(400分割)ではI=16625kN・m^2(99.75%)となります。
このモデルでは,短冊幅を1mにすれば,精算値の1%減と十分な精度を持つものと判断できます。
最近のGenSは,矩形の建物では精算値とし,矩形以外では数値積分によって算出したIを用いて捩れ振動解析を行っています。
検証に用いた粗末なツール(EXCEL)を,“ダウンロード”カテゴリーにアップします。
Tweet
ただし,矩形以外の形状では数値積分する必要があり,十分な精度を確保しようとすると,「細かく床を分割して,かけて,足す」という作業を何百回も繰り返すことになります。プログラム化したくなる計算の代表例ですね。
というのも,約10年前に一貫構造計算結果を元に回転慣性を計算するツールを作りましたが,当時の私は安直に,節点〜重心間距離の自乗に地震用節点重量を乗じて足し合わせました。
これが一貫構造計算結果を用いる上で最も簡便で,質量分布の偏りも表現できる方法だったからです。当時は特に違和感も感じませんでした。
しかし,比較的最近になって・・・
「重心とは対象物の重量中心なんだから,積分する際のrは細かく分けた床の重量中心と床全体の重心との距離でなければおかしい」
「節点重量と節点座標を用いた計算では,rが長くなってしまう」
「柱割りの少ない建物で誤差が大きいんじゃないか」
と思い始めたんです。
そこで,10m角の正方形で4本柱(=4節点),重量は1000kNという簡単なモデルで検証してみます。
質量分布は均質で,重心と図心が一致する(Gx=5m,Gy=5m)とします。
I=1/12×1000kN×(10^2+10^2)=16667kN・m^2(これを精算値とします)
矩形の計算式では簡単にIが求まります。
このモデルで,rを節点位置〜重心間距離として求めると,各節点重量は250kN,距離はXYともに5m(r=7.07m)となり,I=50000kN・m^2になります。精算値の実に3倍です。
こんな極端なモデルは現実には極めて稀でしょうが,やはり柱割りの少ない建物では注意が必要であることがわかります(精算値を超えること事態が明らかに間違いです)。
今度は,積分する際の短冊幅を5m(4分割)とし,分割した各床の重量中心と全体の重心間距離をrとすると,距離はXYともに2.5m(r=3.54m)となり,I=12500kN・m^2(75%)となります。精算値を超えはしませんが,25%減では精度が低すぎます。
短冊幅1m(100分割)ではI=16500kN・m^2(99.00%),0.5m(400分割)ではI=16625kN・m^2(99.75%)となります。
このモデルでは,短冊幅を1mにすれば,精算値の1%減と十分な精度を持つものと判断できます。
最近のGenSは,矩形の建物では精算値とし,矩形以外では数値積分によって算出したIを用いて捩れ振動解析を行っています。
検証に用いた粗末なツール(EXCEL)を,“ダウンロード”カテゴリーにアップします。
Comments